Rango de una función exponencial: Todo lo que necesitas saber

En el mundo de las matemáticas y la estadística, las funciones exponenciales desempeñan un papel fundamental en diversos campos. Una de las características importantes de estas funciones es su rango, que es el conjunto de todos los posibles valores que puede tomar la función. En este artículo, exploraremos en detalle qué es el rango de una función exponencial, cómo se calcula y por qué es importante comprenderlo. ¡Sigue leyendo para descubrir todo lo que necesitas saber sobre este tema fascinante!

Explorando el alcance de la función exponencial

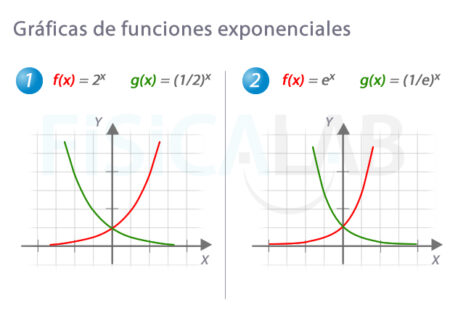
La función exponencial es una de las funciones matemáticas más importantes y útiles en diversos campos como la economía, la física, la ingeniería y la biología. Su forma general es f(x) = a^x, donde "a" es una constante positiva y "x" es la variable independiente.

Idea principal:

La función exponencial tiene la propiedad de crecer o decrecer rápidamente dependiendo del valor de la constante "a". Cuando "a" es mayor que 1, la función crece de manera exponencial, mientras que cuando "a" está entre 0 y 1, la función decrece exponencialmente.

Idea secundaria:

La función exponencial también tiene la propiedad de ser una función continua y suave, lo que la hace ideal para modelar fenómenos que tienen un crecimiento o decrecimiento acelerado en el tiempo.

Algunas aplicaciones de la función exponencial son:

1. Modelar el crecimiento de poblaciones.
2. Describir el decaimiento radioactivo.
3. Calcular el interés compuesto en finanzas.

Explorando las propiedades de una función exponencial

Una función exponencial es una función matemática en la forma de f(x) = a^x, donde "a" es una constante positiva diferente de cero y "x" es una variable. Estas funciones tienen propiedades únicas que las hacen muy útiles en diversas áreas de las matemáticas y la ciencia.

Propiedades de una función exponencial

1. Crecimiento exponencial: Las funciones exponenciales crecen rápidamente a medida que "x" aumenta.
2. Intersección con el eje y: Todas las funciones exponenciales pasan por el punto (0, 1).
3. Asíntota horizontal: Las funciones exponenciales tienen una asíntota horizontal en y=0.
4. Propiedad de la base: Si a > 1, la función se incrementa a medida que x aumenta. Si 0

Explorar las propiedades de una función exponencial puede ayudarnos a comprender mejor su comportamiento y su utilidad en diferentes contextos. Desde el crecimiento de poblaciones hasta el decaimiento radioactivo, las funciones exponenciales nos ofrecen un marco matemático para modelar y comprender fenómenos naturales.

¿Qué otros aspectos de las funciones exponenciales te gustaría explorar?

Explorando el camino de una función exponencial: su comportamiento y propiedades

Una función exponencial es aquella en la que la variable independiente aparece como exponente. Su forma general es f(x) = a^x, donde "a" es la base de la función.

Comportamiento de una función exponencial

Las funciones exponenciales tienen un comportamiento característico: crecen o decrecen muy rápidamente dependiendo del valor de la base. Si la base es mayor que 1, la función crecerá exponencialmente. Si la base está entre 0 y 1, la función decrecerá exponencialmente.

Propiedades de una función exponencial

1. La función exponencial siempre pasa por el punto (0, 1) debido a que cualquier número elevado a la potencia 0 es igual a 1.
2. Las funciones exponenciales son siempre positivas, nunca alcanzan el eje de las x.
3. La función exponencial crece o decrece sin límite a medida que x tiende a más infinito o menos infinito, respectivamente.

Entendiendo la naturaleza de las funciones exponenciales

Las funciones exponenciales son un tipo de función matemática en la que la variable independiente aparece en el exponente. Estas funciones se expresan de la forma f(x) = a^x, donde "a" es la base de la exponencial y "x" es la variable independiente.

Características de las funciones exponenciales:

1. El dominio de una función exponencial es el conjunto de todos los números reales.
2. Las funciones exponenciales crecen de manera exponencial, es decir, aumentan rápidamente a medida que la variable independiente aumenta.
3. La gráfica de una función exponencial tiene una asíntota horizontal en el eje x = 0.

Es importante entender que las funciones exponenciales son útiles en diversos campos como la economía, la biología y la física, ya que modelan crecimientos y decaimientos que ocurren de forma exponencial en la naturaleza.

Recuerda que entender el rango de una función exponencial es fundamental para comprender su comportamiento y aplicaciones en problemas matemáticos y de la vida real. No te quedes solo con conocer la definición, sino practica con ejercicios y situaciones diferentes para afianzar tus conocimientos. ¡No te rindas y sigue aprendiendo! ¡Hasta la próxima!

Si quieres ver otros artículos similares a Rango de una función exponencial: Todo lo que necesitas saber puedes visitar la categoría Educación o revisar los siguientes artículos